When a body is subjected to two equal and opposite forces acting tangentially across the resisting section, as a result of which the body tends to shear off the section, then the stress induced is called shear stress.
The corresponding strain is known as shear strain and it is measured by the angular deformation accompanying the shear stress. The shear stress and shear strain are denoted by the Greek letters tau (τ) and phi (φ) respectively. Mathematically,
Shear stress, τ = Tangential force/Resisting area
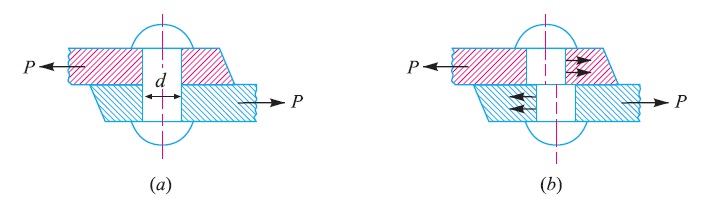
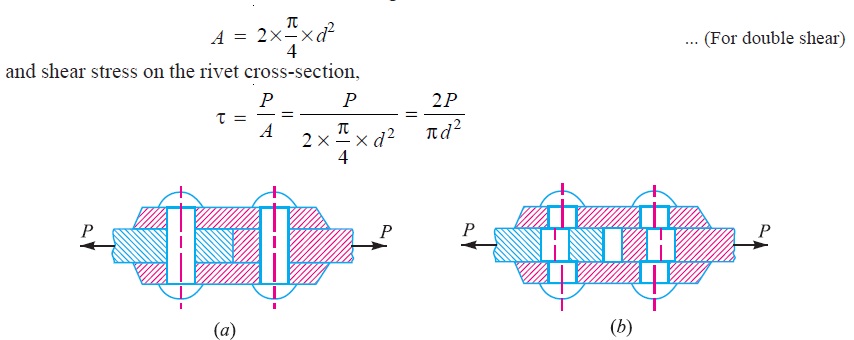
Consider a body consisting of two plates connected by a rivet as shown in Fig. 4.6 (a). In this case, the tangential force P tends to shear off the rivet at one cross-section as shown in Fig. 4.6 (b). It may be noted that when the tangential force is resisted by one cross-section of the rivet (or when shearing takes place at one cross-section of the rivet), then the rivets are said to be in single shear. In such a case, the area resisting the shear off the rivet,
Now let us consider two plates connected by the two cover plates as shown in Fig. 4.1 (a). In this case, the tangential force P tends to shear off the rivet at two cross-sections as shown in Fig. 4.1 (b). It may be noted that when the tangential force is resisted by two cross-sections of the rivet (or when the shearing takes place at two cross-sections of the rivet), then the rivets are said to be in double shear. In such a case, the area resisting the shear off the rivet,
Reference
A textbook of Machine Design by R.S.Khurmi and J.K.Gupta
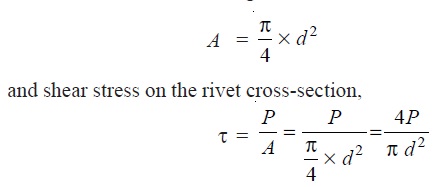










Post Comment
You must be logged in to post a comment.