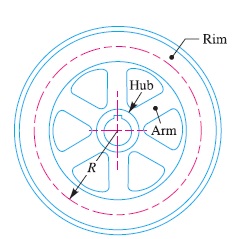
Energy Stored in a Flywheel : A flywheel is shown in Fig. 1. We have already discussed that when a flywheel absorbs energy its speed increases and when it gives up energy its speed decreases.
Let m = Mass of the flywheel in kg,
k = Radius of gyration of the flywheel in metres,
I = Mass moment of inertia of the flywheel about the axis of rotation in kg-m2
= m.k2,
N1 and N2 = Maximum and minimum speeds during the cycle in r.p.m.,
ω1 and ω2 = Maximum and minimum angular speeds during the cycle in rad / s,
N = Mean speed during the cycle in r.p.m. = N1 + N2 /2
ω = Mean angular speed during the cycle in rad / s = ω1+ω2 / 2
Cs = Coefficient of fluctuation of speed = N1-N2/N or ω1-ω2 / ω
We know that mean kinetic energy of the flywheel,
E = 1/2 × I ω^2 = 1/2 ×m k^2 ω^2 (in N-m or joules)
As the speed of the flywheel changes from ω1 to ω2, the maximum fluctuation of energy,
ΔE = Maximum K.E. — Minimum K.E. = (1/2 × I ω1^2)-(1/2 × I ω2^2)
= 1/2 × I ( ω1^2 – ω2^2)
= 1/2 × I ( ω1 + ω2)( ω1 – ω2)
= I.ω (ω1 – ω2) (‘.’ ω = ω1 + ω2/2) ……(i)
= I.ω^2 (ω1 – ω2) /ω …[Multiplying and dividing by ω]
= I.ω^2.Cs = m.k^2.ω^2.Cs …( ‘.’ I = m.k^2) ……(ii)
= 2 E.Cs (‘.’ E = 1/2× I ω^2) ……(iii)
The radius of gyration (k) may be taken equal to the mean radius of the rim (R), because the thickness of rim is very small as compared to the diameter of rim. Therefore substituting k = R in equation (ii), we have
Δ E = m.R^2.ω^2.CS = m.v^2.CS …(Q v = ω.R )
From this expression, the mass of the flywheel rim may be determined.
Notes:
1. In the above expression, only the mass moment of inertia of the rim is considered and the mass moment of inertia of the hub and arms is neglected. This is due to the fact that the major portion of weight of the flywheel is in the rim and a small portion is in the hub and arms. Also the hub and arms are nearer to the axis of rotation, therefore the moment of inertia of the hub and arms is very small.
2. The density of cast iron may be taken as 7260 kg / m3 and for cast steel, it may taken as 7800 kg / m3.
3. The mass of the flywheel rim is given by
m = Volume × Density = 2 π R × A × ρ
From this expression, we may find the value of the cross-sectional area of the rim. Assuming the cross-section of the rim to be rectangular, then
A = b × t
where b = Width of the rim, and
t = Thickness of the rim.
Knowing the ratio of b / t which is usually taken as 2, we may find the width and thickness of rim.
4. When the flywheel is to be used as a pulley, then the width of rim should be taken 20 to 40 mm greater than the width of belt.
Reference A Textbook of Machine Design by R.S. Khurmi and J.K. Gupta
