Length of a Cross Belt Drive
We have discussed that in a cross belt drive, both the pulleys rotate in the opposite directions as shown in Fig. 1.
Let r1 and r2 = Radii of the larger and smaller pulleys,
x = Distance between the centres of two pulleys (i.e. O1O2 ), and
L = Total length of the belt.
Let the belt leaves the larger pulley at E and G and the smaller pulley at F and H as shown in Fig. 1.
Through O2 draw O2M parallel to FE.
From the geometry of the figure, we find that O2M will be perpendicular to O1E.
Let the angle MO2O1 = α radians.
We know that the length of the belt,
L = Arc GJE + EF + Arc FKH + HG
= 2 (Arc JE + FE + Arc FK) …………………(i)
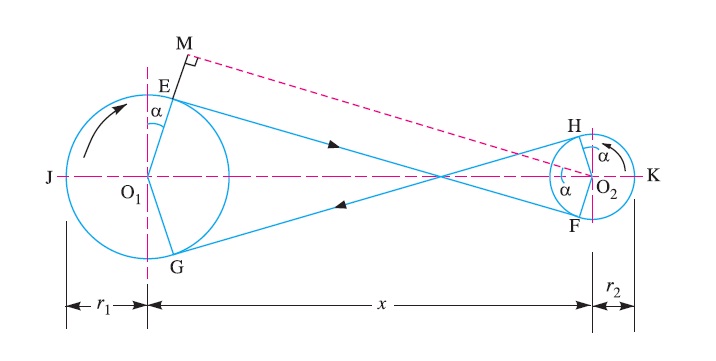
From the geometry of the figure, we find that
sin α = O1M/O1O2 = (O1E + EM)/O1O2 = r1+r2 / x
Since the angle α is very small, therefore putting
sin α = α (in radians) = r1+r2 / x ………………(ii)
.’. Arc JE = r1 (π/2 + α) …………………(iii)
Similarly, arc FK = r2 (π/2 + α) …………………(iv)
and EF = MO2 = [(O1O2 )^2 – (O1M)^2]^0.5 = [x^2 – (r1 + r2 )^2]^o.5
= x [1- (r1+r2 /x)^2]^0.5
Expanding this equation by binomial theorem, we have
EF = x [1- 1/2(r1+r2 /x)^2 + …] = x – [(r1+r2)^2/2x] ……………………(v)
Substituting the values of arc JE from equation (iii), arc FK from equation (iv) and EF from equation (v) in equation (i), we get,
L = 2 [r1(π/2 +α) + x – {(r1+r2)^2/2x} + r2(π/2 +α)]
= 2 [{r1 × π/2} + {r1×α} + x – {(r1+r2)^2/2x} + {r2 × π/2} + {r1×α}]
= 2 [π/2(r1+r2) + α(r1+r2) +x – {(r1+r2)^2/2x}]
= π(r1+r2) + 2α(r1+r2) +2x – {(r1+r2)^2/x}
Substituting the value of α = (r1+r2)/x from equation (ii), we get
L = π(r1+r2) + 2{(r1+r2)/x}{(r1+r2)} +2x – {(r1+r2)^2/x}
= π(r1+r2) + 2{(r1+r2)^2/x} + 2x – {(r1+r2)^2/x}
= π(r1+r2) + 2x + {(r1+r2)^2/x} ……………….. (in terms of pulley radii)
= π(r1+r2) + 2x + {(r1+r2)^2/x} ……………….. (in terms of pulley diameters)
It may be noted that the above expression is a function of (r1 + r2). It is thus obvious, that if sum of the radii of the two pulleys be constant, length of the belt required will also remain constant, provided the distance between centres of the pulleys remain unchanged.
Reference A Textbook of Machine Design by R.S.Khurmi and J.K.Gupta
